FFT 快速傅里叶变换学习笔记

前言

考虑到时间及能力有限，并且诸位大佬写的学习笔记已经是十分详尽，本人目前不可能也不打算写一篇详细度超越各位先人的学习笔记，只是帮助自己理清思路，整理过程并且贯彻一些证明。

自然文章中会有诸多不妥之处，希望各位不吝赐教。

部分比较简单的前置知识就跳过了。

前置知识

复数基本知识
弧度制与三角函数
耐心稳定的心态

FFT 简述

FFT（Fast Fourier Transformation），中文名是 “快速傅里叶离散变换”。

作用是：以 $\mathcal{O(n\log n)}$ 的时间复杂度计算多项式乘法。

在 OI 中的应用：利用卷积思想，化乘为加，加速多项式乘法计算。

卷积

形如 $C[k]=\sum\limits_{i\oplus j=k}A[i]B[j]$ 的式子称为卷积。

多项式乘法就是加法卷积。

多项式的表示

多项式指的是单项式相加组成的代数式。

多项式的系数表示

每一项单项式都有其对应的系数，将系数提炼出来就得到了多项式的系数表示。

一般的，我们把一个 $n-1$ 次的 $n$ 项多项式表示为：

$$f(x)=\sum\limits_{i=0}^{n-1}a_i x^i=a_0x^0+a_1x^1+a_2x^2…+a_{n-1}x^{n-1}$$

系数表示即为：

$$f(x)={a_0.a_1,a_2…a_{n-1}}$$

对于两个 $n$ 项多项式卷积，那么需要枚举每一对系数的乘积结果，复杂度 $\mathcal{O(n^2)}$。

多项式的点值表示

给定 $n+1$ 个互不相同的点，我们可以唯一确定一个 $n$ 次多项式函数。

可以使用 $n+1$ 个点值（有序数对）来描述一个多项式。

点值表示即为：

$$f(x)={(x_0,f(x_0)),(x_1,f(x_1)),(x_2,f(x_2))…(x_n,f(x_n) )}$$

进行乘法即为函数值相乘，复杂度 $\mathcal{O(n)}$。

点值表示远快于暴力卷积。

基本复数运算

说是不讲复数，但是怎么样还是应该说一说。

复数相加为实部虚部对应相加。

相减同理。

相乘形式为：

$$(a+bi)\times (c+di)=ac+adi+bci+bdi^2=(ac-bd)+(ad+bc)i$$

相除形式为：

$$\dfrac{a+bi}{c+di}=\dfrac{(a+bi)(c-di)}{(c+di)(c-di)}=\dfrac{(ac+bd)+(bc-ad)i}{c^2+d^2}=\dfrac{ac+bd}{c^2+d^2}+\dfrac{bc-ad}{c^2+d^2}$$

复数相乘还有一个几何意义：模相乘，角相加。

具体地，$(a_1,\theta_1)(a_2,\theta_2)=(a_1a_2,\theta_1+\theta_2)$。

struct Complex{
    double x,y;
    Complex(){}
    Complex(const double &_x,const double &_y):x(_x),y(_y){};

    inline Complex operator + (const Complex &a)const{
        return Complex(x+a.x,y+a.y);
    }

    inline Complex operator - (const Complex &a)const{
        return Complex(x-a.x,y-a.y);
    }

    inline Complex operator * (const Complex &a)const{
        return Complex(x*a.x-y*a.y,x*a.y+y*a.x);
    }

    inline Complex operator / (const Complex &a)const{
        double tmp=a.x*a.x+a.y*a.y;
        return Complex((x*a.x+y*a.y)/tmp,(y*a.x-x*a.y)/tmp);
    }
}f[maxn],p[maxn];

单位根

概述

$n$ 次单位根 $\omega_n^k$ 是 $n$ 次幂为 $1$ 的复数，即方程 $x^n=1$ 的复数解。

单位根出现在复平面的单位圆上。

$n$ 次单位根 $n$ 等分单位圆。

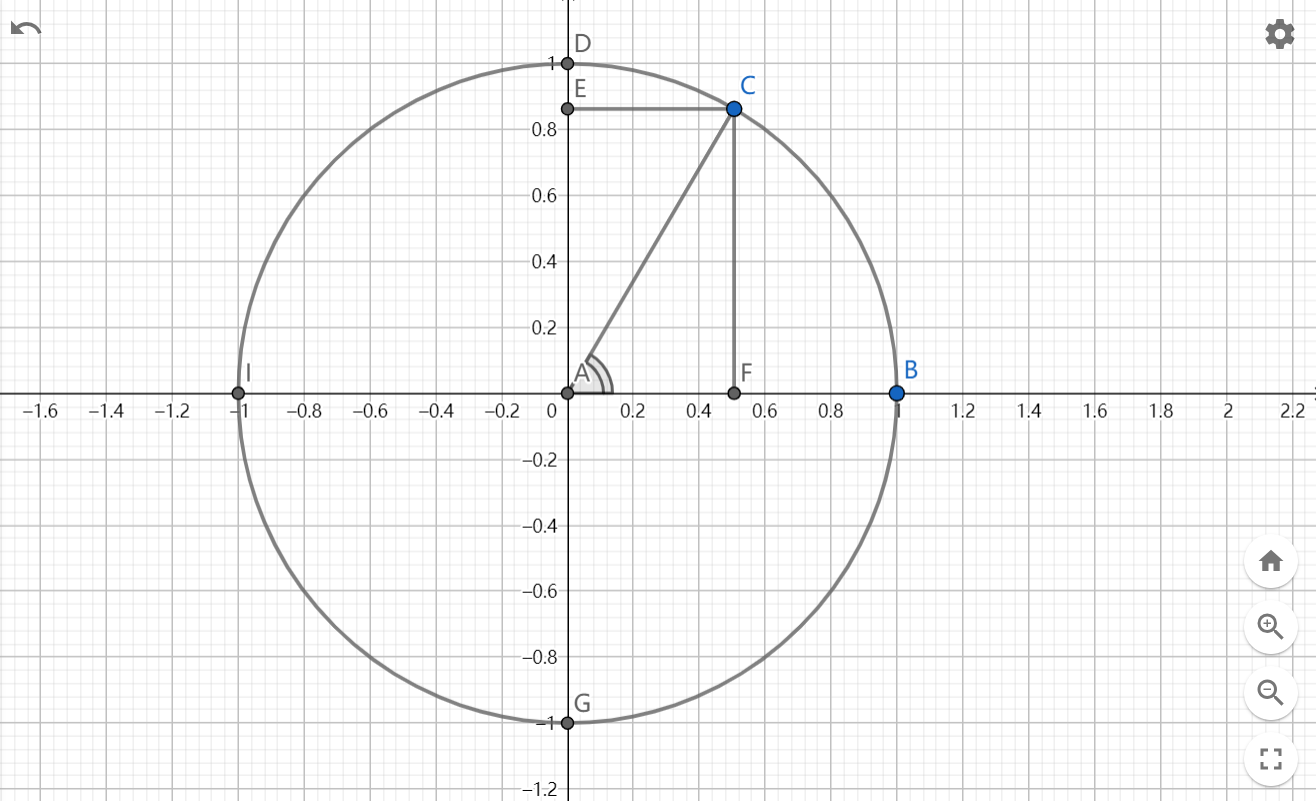
图片来自 @Aw顿顿

对于单位圆上的点，可以表示为 $\cos \theta+i \sin \theta$。

从 $1$ 开始，沿着单位圆逆时针给单位根标号：

$\omega_n^0=1,\omega_n^1$是第二个为单位根…

$\omega_n^k=\cos\frac{k}{n}2\pi+i\sin\frac{k}{n}2\pi$。

性质

$\omega_n^k=\omega_n^{k%n}$
$\omega _n^0=1$
$\omega_n ^k=(\omega_n^1)^k$

（$\omega _n^k=\omega _n^1\times \omega _n^1\times \omega _n^1…\times \omega _n^1$ 共 $k$ 个，可以理解为每次逆时针转动 $\frac{1}{n}$ 个圆周，转了 $k$ 次。或者类比同底数幂相乘）
$\omega_n^j\times \omega_n^k =\omega_n^{j+k}$
$(\omega _n^k)^{-1}=(\omega_n^{-k})=(\omega_n^{n-k})$

可以倒过来反向回推：

$\omega_n^{n-k}\times \omega_n^k=\omega_n^{n-k+k}=\omega_n^n=\omega_n^n=1$

所以 $(\omega _n^k)^{-1}=\omega_n^{n-k}$
$(\omega_n^k)^j=\omega_n^{kj}$
$\omega_{pn}^{pk}=\omega_n^k$

想象成切蛋糕，多切了几刀，但是相应的多取了几倍。
如果 $n$ 是偶数，$\omega_n^{(k+\frac{n}{2})}=-\omega_n^k$

$\omega_n^{(k+\frac{n}{2})}=\omega_n^k\times\omega_n^{(\frac{n}{2})}$

对于 $\omega_n^{(\frac{n}{2})}$ ，可以理解为把幅角转动 $\frac{1}{2}$ 个圆周，关于原点对称。

DFT 与 IDFT 概述

把系数表示转化为点值表示的算法叫做 DFT；

把点值表示转化为系数表示的算法叫做 IDFT（或者称为 DFT 的逆运算）

从系数表示确定点值表示的过程叫做求值，从点值表示确定系数表示的过程叫做插值。

FFT 快速傅里叶变换

FFT 是将系数表示转化为点值表示进行计算，之后再转化成系数表示。

主要过程分为了两步：系数表示转化为点值表示，点值表示转化为系数表示。

就是 DFT 和 IDFT 了。

不使用 FFT 直接进行朴素转化是 $\mathcal{O(n^2)}$ 的。

考虑更高效的方法。

DFT（系数表示转化成点值表示）

设多项式:

$$A(x)=\sum\limits_{i=0}^{n-1}a_i x^i=a_0x^0+a_1x^1+a_2x^2…+a_{n-1}x^{n-1}$$

按奇偶分类（分治思路）：

$$A(x)=(a_0x^0+a_2x^2+a_4x^4…+a_{n-2}x^{n-2})$$

$$+$$

$$(a_1x^1+a_3x^3+a_5x^5…+a_{n-1}x^{n-1})$$

两边统一次数，提出后面的 $x$：

$$A(x)=(a_0+a_2x^2+a_4x^4…+a_{n-2}x^{n-2})$$

$$+$$

$$x\times(a_1+a_3x^2+a_5x^4…+a_{n-1}x^{n-2})$$

设两个 $\frac{n}{2}$ 项的多项式 $L(x)$ 和 $R(x)$ ，考虑降低 $A(x)$ 的次数，执行分治过程：

$$L(x)=(a_0+a_2x^1+a_4x^2…+a_{n-2}x^{\frac{n}{2}-1})$$

$$R(x)=(a_1+a_3x^1+a_5x^2…+a_{n-1}x^{\frac{n}{2}-1})$$

原式可以表示为 $A(x)=L(x^2)+x\times R(x^2)$

注意式子中需要带入 $x^2$ ，由于我们为了执行分治降低了次数，现在要保持式子不变。

之后考虑把单位根 $\omega_n ^k$ 带入原式

$k<\frac{n}{2}$ ，代入 $\omega_n^ k$ :

$$A(\omega_n^k)=L((\omega_n^k)^2)+\omega_n^k\times R((\omega_n^k)^2)$$

根据单位根性质 $7$ $\omega_{pn}^{pk}=\omega_n^k$:

$$(\omega_n^k)^2=(\omega_n^{2k})=(\omega_{\frac{n}{2}}^{k})$$

$$A(\omega_n^k)=L(\omega_{\frac{n}{2}}^{k})+\omega_n^k\times R(\omega_{\frac{n}{2}}^{k})$$

$k<\frac{n}{2}$,代入 $\omega_n^ {k+\frac{n}{2}}$

$$A(\omega_n^ {k+\frac{n}{2}})=L((\omega_n^ {k+\frac{n}{2}})^2)+\omega_n^ {k+\frac{n}{2}}\times R((\omega_n^ {k+\frac{n}{2}})^2)$$

由单位根的性质 $6$ $(\omega_n^k)^j=\omega_n^{kj}$ 得：

$$A(\omega_n^ {k+\frac{n}{2}})=L(\omega_n^ {2k+n})+\omega_n^ {k+\frac{n}{2}}\times R(\omega _n^{2k+n})$$

由单位根的性质 $1$ $\omega_n^k=\omega_n^{k%n}$ 得到：

$$A(\omega_n^ {k+\frac{n}{2}})=L(\omega_n^ {2k})+\omega_n^ {k+\frac{n}{2}}\times R(\omega _n^{2k})$$

由单位根的性质 $7$ $\omega_{pn}^{pk}=\omega_n^k$ 得到：

$$A(\omega_n^ {k+\frac{n}{2}})=L(\omega_{\frac{n}{2}}^ {k})+\omega_n^ {k+\frac{n}{2}}\times R(\omega_{\frac{n}{2}}^ {k})$$

由单位根的性质 $8$ $\omega_n^{(k+\frac{n}{2})}=-\omega_n^k$ 得：

$$A(\omega_n^ {k+\frac{n}{2}})=L(\omega_{\frac{n}{2}}^ {k})-\omega_n^ {k}\times R(\omega_{\frac{n}{2}}^ {k})$$

对比两个式子：

$$A(\omega_n^k)=L(\omega_{\frac{n}{2}}^{k})+\omega_n^k\times R(\omega_{\frac{n}{2}}^{k})$$

$$A(\omega_n^ {k+\frac{n}{2}})=L(\omega_{\frac{n}{2}}^ {k})-\omega_n^ {k}\times R(\omega_{\frac{n}{2}}^ {k})$$

发现右侧只有一个符号的差别。于是他们可以同步计算。

换句话说，FFT 就是把单位根上下半圆的部分分别带入 $A(x)=L(x^2)+x\times R(x^2)$

于是我们在 $\mathcal{O(n\log n)}$ 时间复杂度内完成了系数表示转成点值表示的过程。

IDFT （点值表示转化成系数表示）

由于代入时我们选择了单位根，现在我们十分方便地就可以完成点值表示转化成系数表示。

首先写出结论：把 DFT 中的 $\omega_n^1$ 换成 $\omega_n^{-1}$ 做完之后除以 $n$ 即可。

证明与单位根反演有关。

设多项式 $A(x)$ 经过了 DFT 变换之后得到的点值数列为 $G$。

即 $G=DFT(A)$

回忆代入的过程，可以得到：

$$G[k]=\sum\limits^{n-1}_{i=0}(\omega_n^k)^iA[i]$$

（含义是每一个点值都是把单位根代进每一项中乘以系数得到的）

结论是 $n\times A[k]=\sum\limits^{n-1}_{i=0}(\omega_n^{-k})^iG[i]$

证明：

把点值代入右边可以得到：

$$\sum\limits^{n-1}{i=0}\left( (\omega_n^{-k})G[i] \right)=\sum\limits^{n-1}{i=0}\left( \left( \sum\limits^{n-1}_{j=0}(\omega_n^i)^jA[j] \right) \times(\omega_n^{-k})^i \right)$$

化简得到：

$$\sum\limits^{n-1}{i=0}\left( (\omega_n^{-k})G[i] \right)=\sum\limits^{n-1}{i=0}\left( \sum\limits^{n-1}_{j=0}(\omega_n^{i(j-k)})A[j] \right)$$

分类讨论：

$j=k$

贡献是 $\sum\limits^{n-1}{i=0} \sum\limits^{n-1}{j=0}(\omega_n^{i(j-k)})A[j] \times[j==k]$

$=\sum\limits^{n-1}_{i=0}\omega_n^{i(k-k)}A[k]$

$=\sum\limits^{n-1}_{i=0}A[k]$

$=n\times A[k]$
$j\ne k$

设 $p=j-k$

贡献就是 $\sum\limits_{i=0}^{n-1}\omega_n^{ip}A[k+p]$

$=\omega_n^p\left(\sum\limits_{i=0}^{n-1}\omega_n^{i}\right)A[k+p]$

等比数列求和得到：

$$\left(\sum\limits_{i=0}^{n-1}\omega_n^{i}\right)=\dfrac{1-\omega_n^{np}}{1-\omega_n^{p}}=\dfrac{1-\omega_n^{0}}{1-\omega_n^{p}}=0$$

所以这一部分贡献是 $0$。

这一部分就是所谓的求和引理

证毕。

于是把 $G$ 数列当作系数再代入一遍，单位根换成所谓的 $\omega _n^{-1}$ 就行了。

代码实现

有了上述思路，我们就可以开始着手代码实现了。

补充 $n$ 至 $2$ 的整次幂。

我们上面的过程都是针对 $n$ 是 $2$ 的整次幂进行的，原因是这样可以保证分的足够均匀。

实际中不满足这个条件？补项就行了。在最高次强行添加系数为 $0$ 的项。
预处理单位根

根据单位根的性质 $3$ $\omega_n ^k=(\omega_n^1)^k$，我们可以把他乘 $n$ 次，就能得到所有想要的单位根。

第一个单位根是有的，肯定是 $1$。

第二个单位根 $\omega_n ^1$ 必然是第一个不与实轴重合的单位根，所以他的坐标就是 $(\cos(\frac{2\pi}{n}),\sin(\frac{2\pi}{n}))$
Complex omega(cos(2*Pi/p),sin(2*Pi/p)); for(re int i=0;i<n;i++){ w[i]=buf; buf=buf*omega; }
蝴蝶变换

大概意思是递归版效率太低，我们需要找到迭代解法。

可以发现多项式的第 $i$ 次项到达递归底层时下标为 $i$ 二进制翻转后的数，所以就可以自底向上迭代合并。

可以 $\mathcal{O(n)}$ 递推求出。
for(re int i=0;i<n;i++){ trans[i]=(trans[i>>1]>>1)|((i&1)?n>>1:0); }
具体证明以及详细信息以后再补，今天没时间了。

CODE:

//#define LawrenceSivan

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef unsigned long long ull;

#define INF 0x3f3f3f3f
#define re register

const int maxn=1e7+5;
const int maxm=1;
const double Pi=acos(-1);

struct Complex{
    double x,y;
    Complex(){}
    Complex(const double &_x,const double &_y):x(_x),y(_y){};

    inline Complex operator + (const Complex &a)const{
        return Complex(x+a.x,y+a.y);
    }

    inline Complex operator - (const Complex &a)const{
        return Complex(x-a.x,y-a.y);
    }

    inline Complex operator * (const Complex &a)const{
        return Complex(x*a.x-y*a.y,x*a.y+y*a.x);
    }

    inline Complex operator / (const Complex &a)const{
        double tmp=a.x*a.x+a.y*a.y;
        return Complex((x*a.x+y*a.y)/tmp,(y*a.x-x*a.y)/tmp);
    }
}f[maxn],p[maxn];

int trans[maxn];

int n,m;

inline void FFT(Complex *f,bool op){
    for(re int i=0;i<n;i++){
        if(i<trans[i])swap(f[i],f[trans[i]]);
    }
    for(re int p=2;p<=n;p<<=1){
        int len=p>>1;
        Complex omega(cos(2*Pi/p),sin(2*Pi/p));
        if(!op)omega.y*=-1;
        for(re int k=0;k<n;k+=p){
            Complex buf(1,0);
            for(re int l=k;l<k+len;l++){
                Complex tmp=buf*f[l+len];
                f[l+len]=f[l]-tmp;
                f[l]=f[l]+tmp;
                buf=buf*omega;
            }
        }
    }
}

namespace IO{
    template<typename T>
    inline void read(T &x){
        x=0;T f=1;char ch=getchar();
        while (!isdigit(ch)) {if(ch=='-')f=-1;ch=getchar();}
        while (isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
        x*=f;
    }

    template <typename T, typename... Args>
    inline void read(T& t, Args&... args) {
        read(t); read(args...);
    }

    template<typename T>
    void write(T x){
        if(x<0)putchar('-'),x=-x;
        if(x>9)write(x/10);
        putchar(x%10+'0');
    }

    template<typename T,typename... Args>
    void write(T t,Args... args){
        write(t);putchar(' ');write(args...);
    }
}

using namespace IO;

signed main() {
#ifdef LawrenceSivan
    freopen("aa.in","r", stdin);
    freopen("aa.out","w", stdout);
#endif
    read(n,m);
    for(re int i=0;i<=n;i++)scanf("%lf",&f[i].x);
    for(re int i=0;i<=m;i++)scanf("%lf",&p[i].x);
    for(m+=n,n=1;n<=m;n<<=1);
    for(re int i=0;i<n;i++){
        trans[i]=(trans[i>>1]>>1)|((i&1)?n>>1:0);
    }
    FFT(f,1),FFT(p,1);
    for(re int i=0;i<n;i++)f[i]=f[i]*p[i];
    FFT(f,0);
    for(re int i=0;i<=m;i++)write((int)(f[i].x/n+0.5)),putchar(' ');
    puts("");

    return 0;
}

FFT快速傅里叶变换学习笔记