这两天学了这个。
是轮廓线状压的或许算是裸题。
关键在于怎么压状态。
题意
有一个 $n \times m$ 的棋盘,两个人轮流下棋。
一个位置可以落子当且仅当这个位置的左侧和上面都有棋子。
两个人落在对应的位置会收获各自的贡献值。
最大化自己的得分减去对方的得分。
做法
博弈论?
是有 max_min搜索还有一些别的做法的。
看眼数据范围,都是 $10$ 以内的。
于是考虑状压。
问题随之而来:如何存状态?
由于落子是有限制的,所以需要考虑在什么情况下可以落子。
由于落子是合法的需要满足左边和上边都有棋子,于是在整个过程中必然会有这样的情况:

可以发现这样的轮廓一定是连续的。
于是这就是我们需要的轮廓线。
可以考虑存储右下角的轮廓线作为状态。
如何存储呢?
首先这个轮廓线的长度肯定是 $n+m$ 的。
我们用 $0$ 来表示横边,用 $1$ 来表示竖边。
可以举个例子:
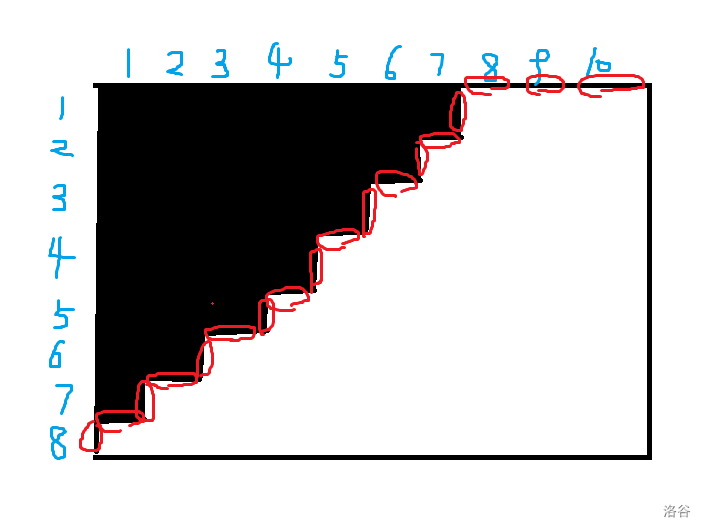
对于当前的状态,从右上角开始,向左下角延伸,如果有横边那么当前位就是 $0$,有竖边就是 $1$;
所以状态串就是 $000101010101010101$
之后对于状态的判断以及转移过程,都可以利用这个轮廓线。
可以发现,经过这样的状压之后,判断是否可以落子的条件就变成了:是否存在一个位置,满足串中有 $01$ 这样的两位,如果有,那么就可以落子。
落子以后,该位置的 $01$ 就会变成 $10$。
对于转移过程中的具体操作,由于需要判断状态串中是否存在 $01$,可以采用一种手法:
|
由于 $3$ 的二进制是 $011$ ,如果也就是判断是否存在 $01$的情况。
之后改变状态:
|
之后起始状态和终止状态就很明显了:
起始状态:$000…00111…11$
终止状态:$111…11000…00$
之后就是关于如何 DP 的问题了。
其实这个事情是不好办的。
首先这个题目要求我们两个人都要走最优策略。
如果按照我们常规的 DP 思路的话,自然是要设 $f[S]$ 为在 $S$ 这个状态下可以获得多少得分差。
但是对于这种博弈论 DP 的题目是不可以这样做的。
由于两方都要采取最优策略,所以我们不得不考虑将来的行动对现在现在的影响。
如果正序 dp 的话也许会发生当前确实取到了最大值但是其实并不是最优策略。
于是我们可以考虑倒过来 dp。
可以假装我们可以一步看到结局,然后选择对自己最有利的状态。
显然棋盘被布满的状态下没有人可以获得新的分数,那么如果我们用 $f[S]$ 表示从 $S$ 轮廓线的状态距离游戏结束还能得多少分。
那么我们会发现,如果这个局面是先手下完以后形成的,那么如何这个局面如何转移的主动权显然是攥在后手的手里,所以此时这个 dp 值应该由所有后继状态的相对于先手最劣的状态转移过来,也就是所有的后继状态取个 $\min$。
如果是后手的话,dp值就应该是对于后手最劣的状态转移过来,也就是所有的后继状态取个 $\max$。
也就是第一个人想要最大化两者的差值,第二个人想要最小化这个差值。
|