Kruskal 重构树

前言

听了 @Wankupi 学长讲了这个东西。

于是就爬过来学了。

确实是很有意思的东西。

不过貌似也很小众，几乎不咋用。

但是性质确实很优美。

特殊的题目也有奇效。

前置知识

Kruskal 算法求解最小生成树。
倍增
主席树

至于为什么需要这些玩意，~~其实并不必要~~

在题目里会用到的。

定义

这个东西我找遍了各大词条，并没有一个合适的定义。

于是可以跳过。

实现过程

在执行 kruskal 的过程中，我们先将边进行排序（排序的方式决定了重构树的性质），之后遍历每一条边，查看这条边的两个端点是否在同一个并查集之内。如果不在，那么就新建一个节点 $node$,这个点的点权等于这条边的边权。

有一张图画的好啊！

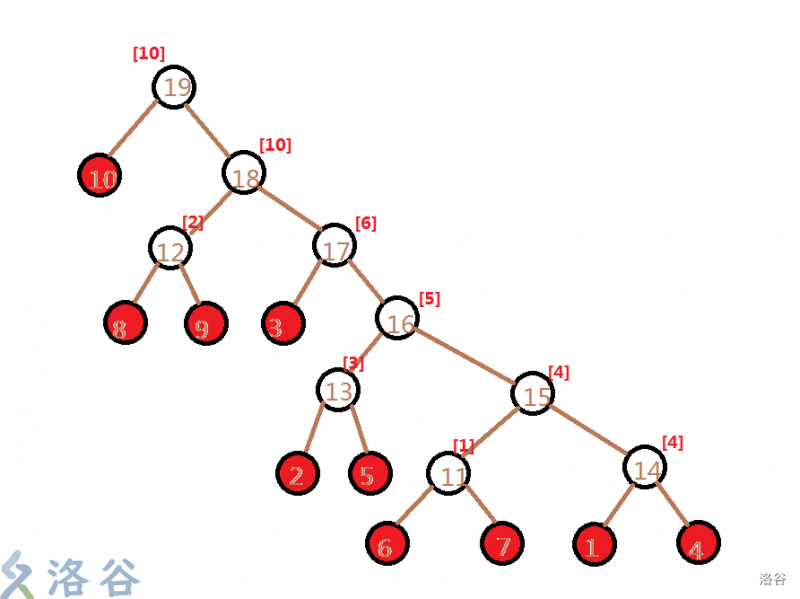
图片来源：@asd369

具体做法：

首先找到两个端点在并查集中的根，之后检查是否在一个并查集中。然后连边就可以了。

namespace Kruskal{
	inline void add(int u,int v){
		nxt[++cnt]=head[u];
		to[cnt]=v;
		head[u]=cnt;
	}
	
	struct node{
		int u,v,dis;
		
		inline bool operator < (const node &a)const{
			return dis<a.dis;
		}
	}e[maxm<<1];

	int ff[maxn];
	
	inline void init(){
		for(re int i=1;i<maxn;i++){
			ff[i]=i;
		}
	}
	
	int find(int x){
		return x==ff[x]?x:ff[x]=find(ff[x]);
	}
	
	int val[maxn<<1],tot;
	
	inline void kruskal(){
		sort(e+1,e+1+m);
		
		init();
		
		for(re int i=1;i<=m;i++){
			int x=find(e[i].u),y=find(e[i].v);
			if(x!=y){
				val[++tot]=e[i].dis;
				ff[x]=ff[y]=ff[tot]=tot;
				add(tot,x);add(tot,y);
				fa[x][0]=fa[y][0]=tot;
			}
		}
	}
	
}

性质

1. Kruskal 重构树是一棵树（~~这不是废话？！~~

而且他还是一棵二叉树（~~虽然看上去也是废话~~

还是一棵有根树，根节点就是最后新建的节点。

1. 若原图不连通，那么建出来的 Kruskal 重构树就是一个森林。
1. 如果一开始按照边权升序排序，那么建出的 Kruskal 重构树就是一个大根堆，反之就是小根堆。
1. 若一开始按照边权升序排序，那么 lca(u,v) 的权值代表了原图中 $u$ 到 $v$ 路径上最大边权的最小值。反之就是最小边权的最大值。
1. Kruskal 重构树中的叶子结点必定是原图中的节点，其余的节点都是原图的一条边。
1. Kruskal 重构树建好以后会比原图多出 $n-1$ 个节点（如果原图联通的话）

一条一条来看：

对于性质 $1$ 和 $2$，比较显然，我们就不说了。

对于性质 $3$ 和 $4$，由于一开始对边权升序排序，所以我们首先遍历到的边一定是权值最小的。

于是对于 Kruskal 重构树中的某一个节点，它的子树中任意一个节点的权值一定小于它本身。

那么可以知道，权值越小的深度越大，权值越大的深度越小。

于是这是大根堆性质。

有了大根堆性质，我们可以发现，由于边权升序，其实就是求解最小生成树的过程，于是能出现在 Kruskal 重构树中的节点必然是要满足也出现在原图的最小生成树中的，那么在找 LCA 的过程中，找到的必然是在 Kruskal 重构树上这条路径中深度最小的点，也就是权值最大的。对于原图来说，这个权值最大的恰好是从 $u$ 到 $v$ 最小值。

若一个点能通过一条路径到达，那么我们走最小生成树上的边也一定能到达该节点。

于是满足了最大值最小的性质。

同理降序也能够得出最小值最大的性质。

对于性质 $5$，可以画图解决。

对于性质 $6$，可以发现，建出 Kruskal 重构树的过程其实也就是求解最小生成树的过程，那么 Kruskal 重构树中新增加的节点数也就是最小生成树中的边数。而最小生成树中的边数最多是 $n-1$ 条，于是 Kruskal 重构树中新增加的节点数也就是 $n-1$ 个。

应用

根据上面的性质们，Kruskal 重构树有几种常见用法：

u->v路径上的最大值最小 or u->v路径上的最小值最大

这就是上面的性质 $3$ 和 $4$ 了。

于是直接套板子就行了。

也给我们一个提示，遇到这种最大值最小或者最小值最大这种类似的语句，可以不急着想二分，还可以想想 Kruskal 重构树。

例题就是 P1967 [NOIP2013 提高组] 货车运输

求解路径上最小值最大。

将边降序排序，建出 Kruskal 重构树，注意处理一下有可能是个森林。

lca 怎么搞都行，不过我喜欢树剖，比较优雅。

查询在 Kruskal 重构树中 lca(u,v） 的权值就好了。

//#define LawrenceSivan

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
#define re register
const int maxn=1e5+5;
#define INF 0x3f3f3f3f

int n,m,tot,q;

struct node{
	int u,v,dis;

	inline bool operator < (const node &a)const{
		return dis>a.dis;
	}
}a[maxn<<1];

int head[maxn],to[maxn<<1],nxt[maxn<<1],cnt;

int val[maxn<<1];

inline void add(int u,int v){
	to[++cnt]=v;
	nxt[cnt]=head[u];
	head[u]=cnt;
}

int dep[maxn],size[maxn],fa[maxn],son[maxn],top[maxn];

bool vis[maxn];

void dfs1(int u,int f){
	size[u]=1;
	vis[u]=true;
	fa[u]=f;
	dep[u]=dep[f]+1;
	for(re int i=head[u];i;i=nxt[i]){
		int v=to[i];
		if(v==f)continue;
		dfs1(v,u);
		size[u]+=size[v];
		if(size[v]>size[son[u]])son[u]=v;
	}
}

void dfs2(int u,int topf){
	top[u]=topf;
	if(!son[u])return;
	dfs2(son[u],topf);
	for(re int i=head[u];i;i=nxt[i]){
		int v=to[i];
		if(v==fa[u]||v==son[u])continue;
		dfs2(v,v);
	}
}

inline int lca(int x,int y){
	while(top[x]!=top[y]){
		if(dep[top[x]]<dep[top[y]])swap(x,y);
		x=fa[top[x]];
	}
	return dep[x]<dep[y]?x:y;
}

int ff[maxn];

int find(int x){
	return x==ff[x]?x:ff[x]=find(ff[x]);
}

inline void init(){
	for(re int i=1;i<maxn;i++){
		ff[i]=i;
	}
}

inline void Kruskal(){
	sort(a+1,a+1+m);

	init();

	for(re int i=1;i<=m;i++){
		int x=find(a[i].u),y=find(a[i].v);
		if(x!=y){
			val[++tot]=a[i].dis;
			ff[tot]=ff[x]=ff[y]=tot;
			add(tot,x);
			add(tot,y);
		}
	} 

	for(re int i=1;i<=tot;i++){
		if(!vis[i]){
			int f=find(i);
			dfs1(f,0);
			dfs2(f,f);
		}
	}
}

inline int read(){
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
    return x*f;
}

int main(){
#ifdef LawrenceSivan
    freopen("aa.in","r",stdin);
    freopen("aa.out","w",stdout);
#endif
    n=read();m=read();tot=n;

    for(re int i=1;i<=m;i++){
    	a[i].u=read();a[i].v=read();a[i].dis=read();
    }

    Kruskal();

    q=read();
    while(q--){
		int u=read(),v=read();
		if(find(u)!=find(v))puts("-1");
		else printf("%d\n",val[lca(u,v)]);
    }



	return 0;
}

从 u 出发只经过边权不超过 x 的边能到达的节点

根据性质 $3$，可以发现，只需要找到边权升序的 Kruskal 重构树中找到深度最小的，点权不超过 $x$ 的节点，那么这个节点的子树即为所求。

找这个点一般用树上倍增

我不要！！！！~~树剖党声嘶力竭~~

没办法这玩意还是倍增好

我们考虑当前我们找到的这个节点为 $x$，然后我们倍增枚举它的祖先，由于是升序排序，所以它祖先的点的点权必然大于等于它的点权，于是，我们倍增的时候只要判断如果它的祖先的点权就好了。

inline void kruskal(){
		sort(e+1,e+1+m);
		
		init();
		
		for(re int i=1;i<=m;i++){
			int x=find(e[i].u),y=find(e[i].v);
			if(x!=y){
				val[++tot]=e[i].dis;
				ff[x]=ff[y]=ff[tot]=tot;
				add(tot,x);add(tot,y);
				fa[x][0]=fa[y][0]=tot;
			}
		}
		dfs(tot);
	}


namespace BIN{
	int fa[maxn<<1][21],range[maxn<<1][2];

	void dfs(int u){
		for(re int i=1;i<=20;i++){
			fa[u][i]=fa[fa[u][i-1]][i-1];
		}
		
		...
	}
}

int main(){
	while(q--){
		int u=read(),x=read();
		for(re int i=20;~i;i--){
			if(fa[u][i]&&val[fa[u][i]]<=x)v=fa[u][i];
		}
	}
}

大概就是这样的。

例题：P4197 Peaks

这个题其实也能用线段树合并做。

其实这个题在题单里躺了好久了，本来是打算线段树合并做的，然后学了重构树于是就用重构树了。

主体思路是裸的，多出来的就是一个第 $k$ 大。

~~这就是为啥我说需要主席树当做前置知识~~

然后子树区间第 $k$ 大，dfs 序 + 主席树大力维护就行了。

码农题，不好，思维题，好！

~~但是思维题不会做嘤嘤嘤~~

其实还是有很多细节问题的。

首先问题就是关于无解情况的判断。

肯定是对于一个满足条件的子树，子树中节点个数不足 $k$ 个。

需要注意的是，由于 Kruskal 重构树的性质 $5$，我们知道在 Kruskal 重构树中只有叶子节点才是会对答案产生贡献的，于是我们需要统计的子树大小并不是我们以往统计的那样，而是只统计叶子节点。

实现也很简单：

void dfs(int u){
    for(re int i=head[u];i;i=nxt[i]){
        int v=to[i];
        if(v==fa[u][0])continue;
        fa[v][0]=u;
        dfs(v);
        size[u]+=size[v];
    }
    if(!size[u])size[u]=1;
}

剩下的部分其实就好说很多了。

注意一下离散化就行了。

//#define LawrenceSivan

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
#define re register
const int maxn=2e5+5;
const int maxm=5e5+5;
#define INF 0x3f3f3f3f

int n,m,q,tmp,num;

int a[maxn],b[maxn]; 

int head[maxn<<1],to[maxn<<1],nxt[maxn<<1],cnt;


namespace SegmentTree{
    inline void Discretization(){
        sort(b+1,b+1+n);
        tmp=unique(b+1,b+1+n)-b-1;
        for(re int i=1;i<=n;i++)a[i]=lower_bound(b+1,b+1+tmp,a[i])-b;
    }

    struct SegmentTree{
        int lc,rc,v;
        #define ls(x) st[x].lc
        #define rs(x) st[x].rc
    }st[maxn<<6];

    int segtot,root[maxn<<1];

    void build(int &rt,int l,int r){
        rt=++segtot;
        if(l==r)return;

        int mid=(l+r)>>1;
        build(ls(rt),l,mid);
        build(rs(rt),mid+1,r);
    }

    int modify(int rt,int l,int r,int x){
        int t=++segtot;
        ls(t)=ls(rt),rs(t)=rs(rt);
        st[t].v=st[rt].v+1;

        if(l==r)return t;

        int mid=(l+r)>>1;
        if(x<=mid)ls(t)=modify(ls(t),l,mid,x);
        else rs(t)=modify(rs(t),mid+1,r,x);

        return t;
    }

    int query(int x,int y,int l,int r,int k){
        int xx=st[rs(y)].v-st[rs(x)].v;

        if(l==r)return l;

        int mid=(l+r)>>1;
        if(k<=xx)return query(rs(x),rs(y),mid+1,r,k);
        else return query(ls(x),ls(y),l,mid,k-xx);
    }
    
}

using namespace SegmentTree;

namespace BIN{
    int fa[maxn<<1][30],pos[maxn<<1],st1[maxn<<1],ed[maxn<<1],size[maxn<<1];

    void dfs(int u){
        pos[++num]=u;st1[u]=num;
        for(re int i=1;i<=25;i++){
            fa[u][i]=fa[fa[u][i-1]][i-1];
        }
        for(re int i=head[u];i;i=nxt[i]){
            int v=to[i];
            if(v==fa[u][0])continue;
            fa[v][0]=u;
            dfs(v);
            size[u]+=size[v];
        }
        if(!size[u])size[u]=1;
        ed[u]=num;
    }
}

using namespace BIN;

namespace Kruskal{
    inline void add(int u,int v){
        nxt[++cnt]=head[u];
        to[cnt]=v;
        head[u]=cnt;
    }
    
    struct node{
        int u,v,dis;
        
        inline bool operator < (const node &a)const{
            return dis<a.dis;
        }
    }e[maxm];

    int ff[maxn<<1];
    
    inline void init(){
        for(re int i=1;i<maxn;i++){
            ff[i]=i;
        }
    }
    
    int find(int x){
        return x==ff[x]?x:ff[x]=find(ff[x]);
    }
    
    int val[maxn<<1],tot;

    inline void kruskal(){
        sort(e+1,e+1+m);
        
        init();
        
        for(re int i=1;i<=m;i++){
            int x=find(e[i].u),y=find(e[i].v);
            if(x!=y){
                val[++tot]=e[i].dis;
                ff[x]=ff[y]=ff[tot]=tot;
                add(tot,x);add(tot,y);
            }
        }
        
        dfs(tot);
    }
    
}

using namespace Kruskal;

inline int read(){
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
    return x*f;
}

int main(){
#ifdef LawrenceSivan
    freopen("aa.in","r",stdin);
    freopen("aa.out","w",stdout);
#endif
    n=read();m=read();q=read();tot=n;
    for(re int i=1;i<=n;i++){
        a[i]=b[i]=read();
    }

    Discretization();
    
    for(re int i=1;i<=m;i++){
        e[i].u=read();
        e[i].v=read();
        e[i].dis=read();
    }
    
    kruskal();

    for(re int i=1;i<=tot;i++){
        root[i]=root[i-1];
        if(pos[i]<=n)root[i]=modify(root[i-1],1,tmp,a[pos[i]]);
     }
    
    while(q--){
        int v=read(),x=read(),k=read();
        for(re int i=25;~i;i--){
            if(fa[v][i]&&val[fa[v][i]]<=x)v=fa[v][i];
        }
        if(size[v]<k){
            puts("-1");
            continue;
        }
        else printf("%d\n",b[query(root[st1[v]-1],root[ed[v]],1,tmp,k)]);
    }
    
    
    return 0;
}

看了题解以后发现这题也可以不使用 dfs 序，由于每个节点直接对应一个区间，所以可以直接处理。

注意区间是左开右闭的。

//#define LawrenceSivan

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
#define re register
const int maxn=1e5+5;
const int maxm=5e5+5;
#define INF 0x3f3f3f3f

int n,m,q,tmp,num;

int a[maxn],b[maxn]; 

int head[maxn<<1],to[maxm<<1],nxt[maxm<<1],cnt;

namespace SegmentTree{
	inline void Discretization(){
		sort(b+1,b+1+n);
		tmp=unique(b+1,b+1+n)-b-1;
		for(re int i=1;i<=n;i++)a[i]=lower_bound(b+1,b+1+tmp,a[i])-b;
	}

	struct SegmentTree{
		int lc,rc,v;
		#define ls(x) st[x].lc
		#define rs(x) st[x].rc
	}st[maxn<<5];

	int segtot,root[maxn];

	void build(int &rt,int l,int r){
		rt=++segtot;
		if(l==r)return;

		int mid=(l+r)>>1;
		build(ls(rt),l,mid);
		build(rs(rt),mid+1,r);
	}

	int modify(int rt,int l,int r,int x){
		int t=++segtot;
		ls(t)=ls(rt),rs(t)=rs(rt);
		st[t].v=st[rt].v+1;

		if(l==r)return t;

		int mid=(l+r)>>1;
		if(x<=mid)ls(t)=modify(ls(t),l,mid,x);
		else rs(t)=modify(rs(t),mid+1,r,x);

		return t;
	}

	int query(int x,int y,int l,int r,int k){
		int xx=st[rs(y)].v-st[rs(x)].v;

		if(l==r)return l;

		int mid=(l+r)>>1;
		if(k<=xx)return query(rs(x),rs(y),mid+1,r,k);
		else return query(ls(x),ls(y),l,mid,k-xx);
	}
	
}

using namespace SegmentTree;

namespace BIN{
	int fa[maxn<<1][21],range[maxn<<1][2];

	void dfs(int u){
		for(re int i=1;i<=20;i++){
			fa[u][i]=fa[fa[u][i-1]][i-1];
		}
		range[u][0]=num;
		if(!head[u]){
			range[u][1]=++num;
			root[num]=modify(root[num-1],1,tmp,a[u]);
			return;
		}
		for(re int i=head[u];i;i=nxt[i]){
			int v=to[i];
			dfs(v);
		}
		range[u][1]=num;
	}
}

using namespace BIN;

namespace Kruskal{
	inline void add(int u,int v){
		nxt[++cnt]=head[u];
		to[cnt]=v;
		head[u]=cnt;
	}
	
	struct node{
		int u,v,dis;
		
		inline bool operator < (const node &a)const{
			return dis<a.dis;
		}
	}e[maxm<<1];

	int ff[maxn];
	
	inline void init(){
		for(re int i=1;i<maxn;i++){
			ff[i]=i;
		}
	}
	
	int find(int x){
		return x==ff[x]?x:ff[x]=find(ff[x]);
	}
	
	int val[maxn<<1],tot;
	
	inline void kruskal(){
		sort(e+1,e+1+m);
		
		init();
		
		for(re int i=1;i<=m;i++){
			int x=find(e[i].u),y=find(e[i].v);
			if(x!=y){
				val[++tot]=e[i].dis;
				ff[x]=ff[y]=ff[tot]=tot;
				add(tot,x);add(tot,y);
				fa[x][0]=fa[y][0]=tot;
			}
		}
		build(root[0],1,tmp);
		dfs(tot);
	}
	
}

using namespace Kruskal;

inline int read(){
    int x=0,f=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
    while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
    return x*f;
}

int main(){
#ifdef LawrenceSivan
    freopen("aa.in","r",stdin);
    freopen("aa.out","w",stdout);
#endif
	n=read();m=read();q=read();tot=n;
	for(re int i=1;i<=n;i++){
		a[i]=b[i]=read();
	}

	Discretization();
	
	for(re int i=1;i<=m;i++){
		e[i].u=read();
		e[i].v=read();
		e[i].dis=read();
	}
	
	kruskal();
	
	while(q--){
		int v=read(),x=read(),k=read();
		for(re int i=20;~i;i--){
			if(fa[v][i]&&val[fa[v][i]]<=x)v=fa[v][i];
		}
		if(range[v][1]-range[v][0]<k){
			puts("-1");
			continue;
		}
		else printf("%d\n",b[query(root[range[v][0]],root[range[v][1]],1,tmp,k)]);
	}
	
	
	return 0;
}

Kruskal 重构树总结

Kruskal 重构树

前言

前置知识

定义

实现过程

性质

应用

u->v路径上的最大值最小 or u->v路径上的最小值最大

从 u 出发只经过边权不超过 x 的边能到达的节点

P4363 [九省联考2018]一双木棋chess（轮廓线状压）

树上差分总结

LawrenceSivan