CF545E Paths and Trees
前言:
学这个的时候看了一些博客,感觉其实这一块网上很多博客和题解其实一些细节没有说太清楚。于是今天主要想说一下关于最短路径树的一些细节与处理问题。
最短路径树
$SPT$,就是从一张连通图中,有树满足从根节点到任意点的路径都为原图中根到任意点的最短路径的树。
$SBT$ 有以下特点:
与最小生成树的区别:最小生成树只需要满足全图联通就可以了。
这个问题这篇日报写的很清楚。
一般用 Dijkstra 实现。
大家都知道, Dijkstra 实现过程就像是一条一条把边拉进来,于是我们只需要在松弛操作的时候记录一下前驱就可以了。
这个与一般的 Dijkstra 无异。
int pre[maxn];
bool vis[maxn];
ll dis[maxn],ans[maxn];
#define P pair<ll,int>
#define mp make_pair
inline void Dijkstra(int s){
priority_queue <P,vector<P>,greater<P> > q;
memset(vis,0,sizeof(vis));
memset(dis,0x3f,sizeof(dis));
dis[s]=0;
q.push(mp(0,s));
while(!q.empty()){
int x=q.top().second;q.pop();
if(vis[x])continue;
vis[x]=true;
for(re int i=head[x];i;i=nxt[i]){
int v=to[i];
if(dis[v]>=dis[x]+w[i]){
dis[v]=dis[x]+w[i];
pre[v]=i;
q.push(mp(dis[v],v));
}
}
}
}
|
复杂度 $O((n+m)logn)$
细节部分
$1$:关于这道题的题目要求(权值和最小):
如何考虑
给定一张带正权的无向图和一个源点,求边权和最小的最短路径树。
要求我们求出边权和最小的。
可以画图理解:
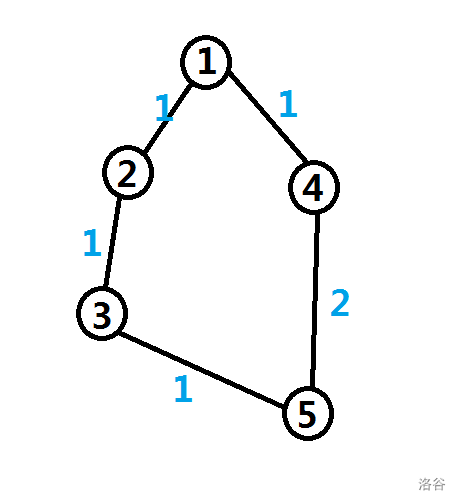
显然,从节点 $1$ 到 节点 $5$ 有两条路径都是最短的。
如果选择 $1->2->3->5$ 这一条,那么最短路树长这个样子:
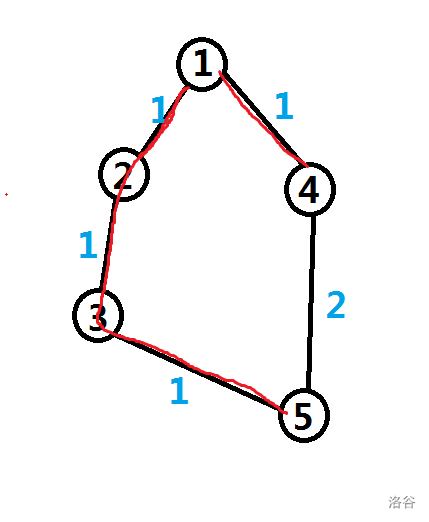
权值和是 $1+1+1+1=4$.
如果选择 $1->4->5$ 这一条,最短路树长这样:
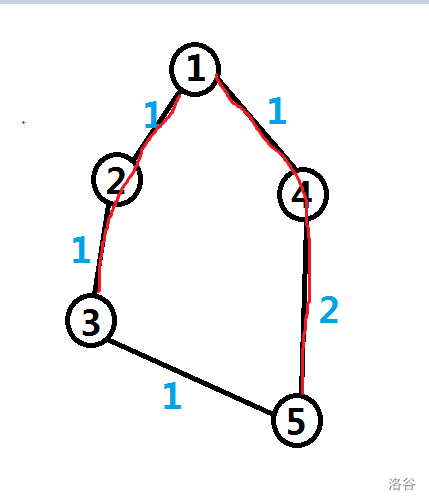
权值和是 $1+1+1+2=5$.
根据题意,选择上面那一种。
为什么?
我们反向考虑:
当我们找到一个节点,发现有两条路径都是最短路,为了求最短路径树,必然只有一条路能被选到,也就是说,一个边会成为树边,另一个就是非树边,而最短路径树权值和最小是针对树边而言的,于是我们选择的问题就集中在连接这个点的两条边哪一个更小,并使之成为树边。
有的题解会这么写:
为了满足本题的要求,还要生成树边权最小。自然是两点间路程相等情况下,经过的边数越多越好
其实这是不正确的。
通过一张图来看:
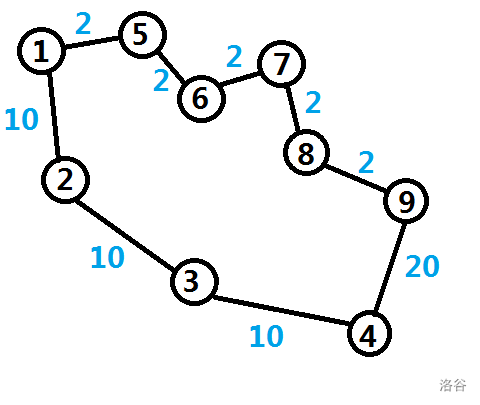
可以发现,从节点 $1$ 到节点 $4$ 的最短路有两条。
路线一 $1->2->3->4$ ,边数是 $3$,
路线二 $1->5->6->7->8->9->4$ , 边数是 $6$.
若选择路线一:
最短路树:
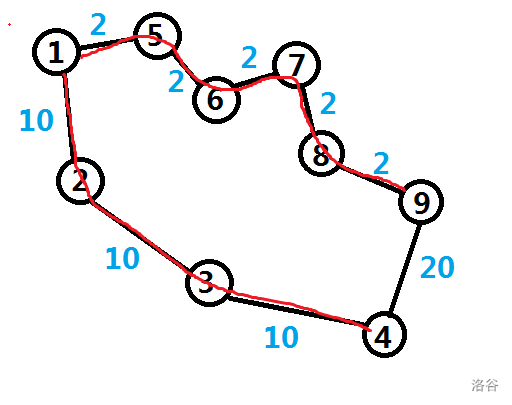
权值和为 $10+10+10+2+2+2+2+2=40$.
若选择路线二:
最短路树:
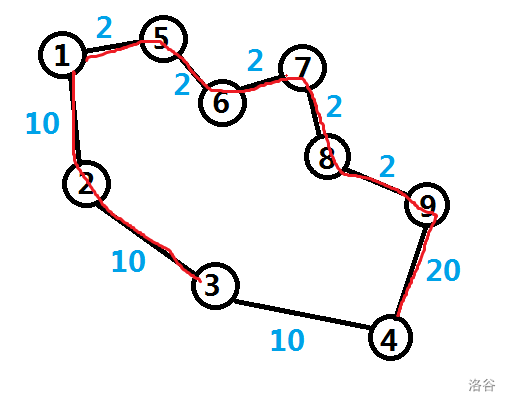
权值和为 $10+10+2+2+2+2+2+20=50$.
代码实现
在满足这个问题的时候,大部分题解都会这么写:
for(re int i=head[x];i;i=nxt[i]){
int v=to[i];
if(dis[v]>dis[x]+w[i]){
dis[v]=dis[x]+w[i];
pre[v]=i;
q.push(mp(dis[v],v));
}
else if(dis[v]==dis[x]+w[i]&&w[i]<w[pre[v]])pre[v]=i;
}
|
就是说他们把权值相等时单独拿出来进行判断,进行松弛的时候如果松弛前的结果与松弛后的结果相等即 $dis[now]=dis[next]+w$,比较连接这条点的边的大小,即 $w[i]$ 与 $w[pre[next]]$ ,如果 $w[i]<w[pre[next]]$,那么更新当前的 $pre$ 。
其实这是完全没必要的。
画图理解:

假如现在只有一个点没有在最短路树中。
由于我们使用的是堆优化的 Dijkstra ,所以率先被扩展出来的点的 $dis$ 一定是更小的。
比如上图中,如果想要扩展到 $5$ ,那么只能从 $3$ 或者 $4$ 而来。
$dis[4]=1$ ,$dis[3]=2$ ,$dis[4]<dis[3]$, 显然是 $4$ 先扩展出来,然后才能扩展 $5$ 。
又因为他们的路径权值是一样的,这只能说明 连接 $3,5$ 的边的权值是小于连接 $4,5$ 的边的权值的。
根据上面的内容,我们需要选择 $3->5$ 这个边。
于是可以发现:
在最短路相等的情况下,扩展到同一个节点,后出堆的点连的边权值一定更小
所以我们直接就可以省去分类讨论的功夫,直接把他们写在一起:
for(re int i=head[x];i;i=nxt[i]){
int v=to[i];
if(dis[v]>=dis[x]+w[i]){
dis[v]=dis[x]+w[i];
pre[v]=i;
q.push(mp(dis[v],v));
}
}
|
$2$:关于边的 $id$ 记录
也有一些同志写的时候喜欢记录一下边的 $id$ ,虽然这样做也可以,但是我个人更喜欢另外一种方式:在循环的时候直接用 $i$ 来作为 $id$ ,这样做会省下一些空间虽然这些空间完全没有省下的必要
单独开 $id$ :
int head[maxn],to[maxn<<1],nxt[maxn<<1],id[maxn<<1],cnt;
ll w[maxn<<1];
inline void add(int u,int v,ll val,int i){
nxt[++cnt]=head[u];
to[cnt]=v;
w[cnt]=val;
id[cnt]=i;
head[u]=cnt;
}
int main(){
n=read();m=read();k=read();
for(re int i=1,u,v;i<=m;i++){
ll val;
u=read();v=read();val=read();
add(u,v,val,i);
add(v,u,val,i);
}
...
}
|
用循环变量索引:
int head[maxn],to[maxn<<1],nxt[maxn<<1],cnt;
ll w[maxn<<1];
inline void add(int u,int v,ll val){
nxt[++cnt]=head[u];
to[cnt]=v;
w[cnt]=val;
head[u]=cnt;
}
int main(){
n=read();m=read();k=read();
for(re int i=1,u,v;i<=m;i++){
ll val;
u=read();v=read();val=read();
add(u,v,val);
add(v,u,val);
}
...
}
|
但是需要注意的是,如果单独开一个 $id$ 数组用来记录 $id$ 的话,那么最后 $dfs$ 的时候 $id$ 就直接是答案了。
但是如果使用循环变量 $i$ 来进行索引,那么最后得出答案时需要 $(ans[i]+1)/2)$.
具体原因也很好想。
单独记录 $id$ 的话,双向边的 $id$ 是一样的,而循环变量索引却导致两条双向边 $id$ 不一样。
单独开 $id$ :
void dfs(int u){
if(tot>=k)return;
vis[u]=true;
for(re int i=head[u];i;i=nxt[i]){
int v=to[i],pos=id[i];
if(vis[v])continue;
if(dis[v]==dis[u]+w[i]){
ans[++h]=pos;
tot++;
dfs(v);
if(tot>=k)return;
}
}
}
int main(){
...
dfs(1);
for(re int i=1;i<=h;i++){
printf("%d ",ans[i]);
}
}
|
用循环变量索引:
void dfs(int u){
if(tot>=k)return;
vis[u]=true;
for(re int i=head[u];i;i=nxt[i]){
int v=to[i];
if(vis[v])continue;
if(dis[v]==dis[u]+w[i]){
ans[++h]=i;
tot++;
dfs(v);
if(tot>=k)return;
}
}
}
int main(){
...
dfs(1);
for(re int i=1;i<=h;i++){
printf("%d ",(ans[i]+1)/2);
}
}
|
$3$:关于输出问题
这个题完全不用排序啊。
You may print the numbers of the edges in any order.
If there are multiple answers, print any of them.
虽然题目翻译没说这个问题,但是关于输入输出的英文原文还是要看看的吧。
不太懂为什么别的题解要排一遍序。
long long 还是要开的。
CODE:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define re register
const int maxn=3e5+5;
#define INF 0x3f3f3f3f3f3f3f3f
int head[maxn],to[maxn<<1],nxt[maxn<<1],cnt;
ll w[maxn<<1];
inline void add(int u,int v,ll val){
nxt[++cnt]=head[u];
to[cnt]=v;
w[cnt]=val;
head[u]=cnt;
}
int pre[maxn];
bool vis[maxn];
ll dis[maxn],ans[maxn];
#define P pair<ll,int>
#define mp make_pair
inline void Dijkstra(int s){
priority_queue <P,vector<P>,greater<P> > q;
memset(vis,0,sizeof(vis));
memset(dis,0x3f,sizeof(dis));
dis[s]=0;
q.push(mp(0,s));
while(!q.empty()){
int x=q.top().second;q.pop();
if(vis[x])continue;
vis[x]=true;
for(re int i=head[x];i;i=nxt[i]){
int v=to[i];
if(dis[v]>=dis[x]+w[i]){
dis[v]=dis[x]+w[i];
pre[v]=i;
q.push(mp(dis[v],v));
}
}
}
}
int n,m,s;
inline ll read(){
ll x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
return x*f;
}
int main(){
#ifdef LawrenceSivan
freopen("aa.in","r",stdin);
freopen("aa.out","w",stdout);
#endif
n=read();m=read();
for(re int i=1,x,y;i<=m;i++){
ll val;
x=read();y=read();val=read();
add(x,y,val);
add(y,x,val);
}
s=read();
Dijkstra(s);
ll sum=0,tot=0;
for(re int i=1;i<=n;i++){
if(i==s)continue;
int pos=pre[i];
sum+=w[pos];
ans[++tot]=pos;
}
printf("%lld\n",sum);
for(re int i=1;i<=tot;i++){
printf("%lld ",(ans[i]+1)/2);
}
return 0;
}
|