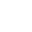我们都知道，线段树是一种效率较高的数据结构。但是它有一个缺点，就是我们需要的空间比较大。对于权值线段树，如果我们的值域比较大，那么我们所需要的空间就是惊人的，于是我们需要采取一些策略来解决这个问题。

在线段树的应用过程中，我们可以发现，在每次修改与查询操作的时候，我们只需要针对从根节点开始最多的 $log(n)$ 个节点进行操作就可以了，那么可以发现其他的很多节点其实并没有用上，那么我们可不可以在用到某一个区间的时候动态地把他开出来而不是一次性全部开出来呢？

答案是肯定的，我们完全可以在一开始开出一个根节点代表$[1-n]$，在需要用到某个区间的时候再把这个区间所对的节点开出来供我们使用。

这样的话，可以发现我们舍弃了线段树的二倍编码原则，而是采用用变量记录形式来记录编号，并且在递归访问的时候，把每个节点代表的区间作为参数传递。

struct node{
	int ls,rs;
	int data;
}st[maxn<<1];

int cnt;
int build(){
	cnt++;
	st[cnt].ls=st[cnt].rs=st[cnt].data=0;
	return cnt;
}

动态开点线段树比较好的例题是 P3960 [NOIP2017 提高组] 列队

经过观察我们可以发现，每次离队所影响的最多只是当前位置还有这一排的最后一个位置以及最后一列最后一行的位置；

于是我们可以考虑用一个支持单点修改的线段树，建立$n + 1$棵，前$n$棵代表第$n$行前$m - 1$个答案，第$n+1$棵表示最后一列。

第一步：我们所操作的是一个长相很规整的的矩形，根据题目的操作要求，我们可以将其分为n+1个区间，即$n \times m$的矩形分为，$n \times (m-1)$的矩形和$1 \times n$ 的矩形，红色的矩形每一行算作一个区间，最后蓝色的一列独自成为一个区间，一共$n+1$个区间。

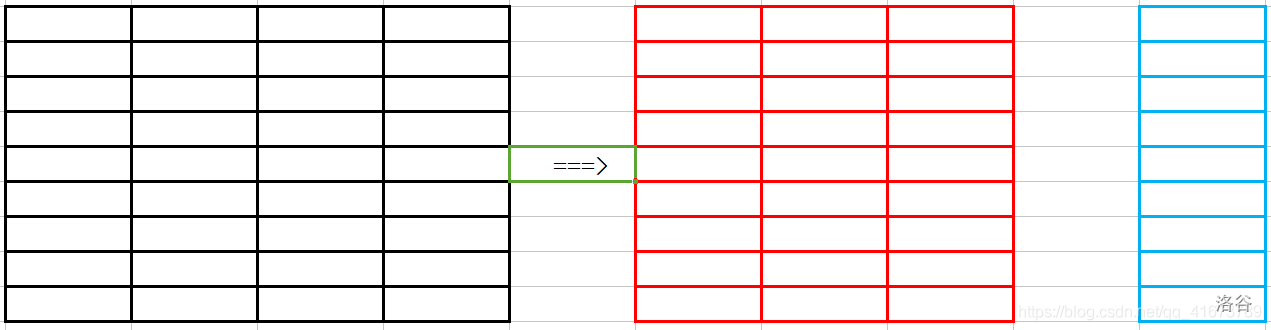
axujukr0.png

每我们的操作就是从所有红区间中，当输入x,y时，即代表我们要将第$x4=$的红区间的第$y$个数取出来，$[y+1,m]$的数往前挪一位，然后蓝区间的第$x$个数就会空出，然后将蓝区间的$[x+1,n]$的数往前挪一位，蓝区间的最后一位，也就是整个矩形的右下角会空出，最后，将取出的数放入右下角这个空即可

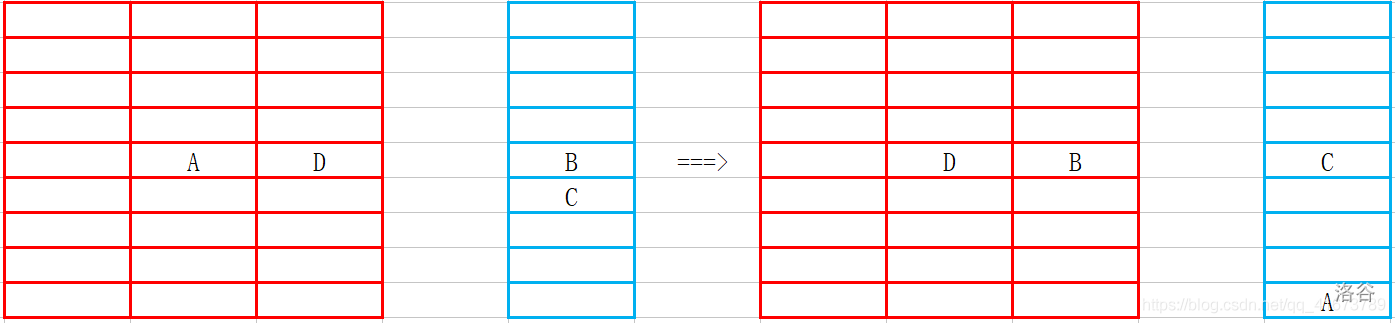
4at8sjkv.png

第二步：我们因为此时的区间不是在移动就是在提取，所以是维护区间，所以自然想到了线段树，因为是维护多个区间，即多个根。所以此时要用到主席树.

第三步：一个区间约有$n$个数，如果每个数都往前挪一位，$q$次询问，每次询问带有$n$次挪移，那么我们考虑不挪动，而是给即将空出来的位置打上标记，表示这个数已经被用过，因为区间最后会再加一个数进来，所以区间长度不变。两种方式最后留下的区间等价

081t1gd4.png

CODE：

//#define LawrenceSivan

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef unsigned long long ull;
#define re register
const int maxn=3e5+5;

int n,m,q,now;
int cnt,Max;

ll ans;

struct node{
	int ls,rs,size;//size:当前区间内有多少个数没有被标记
	ll val;
	
	node(){}
	node(const int _ls,const int _rs,const int _size,const ll _val):
		ls(_ls),rs(_rs),size(_size),val(_val){}
}st[maxn<<5];//严格来讲应该开 Q * log2(N)，也就是20倍 ，为了方便与保险，我们直接开32倍

int ins[maxn],root[maxn];
//ins[i]记录第i棵树插入了多少个新数
//root[i]记录第i棵树的根节点

inline int len(int l,int r){
	if(now==n+1){
		if(r<=n)return r-l+1;
		if(l<=n)return n-l+1;
		return 0;
	}
	if(r<m)return r-l+1;
	if(l<m)return (m-1)-l+1;
	
	return 0;
}

ll query(int &rt,int l,int r,int pos){
	if(!rt){//动态开点
		rt=++cnt;
		st[rt].size=len(l,r);
		
		if(l==r){
			if(now==n+1)st[rt].val=1ll*l*m;
			else st[rt].val=1ll*(now-1)*m+l;
		}
	}
	st[rt].size--;这个区间有一个数被取出
	if(l==r)return st[rt].val;
	
	int mid=(l+r)>>1;
	if(!st[rt].ls &&len(l,mid)>=pos||st[st[rt].ls].size>=pos){
		query(st[rt].ls,l,mid,pos);
	}
	else{
		int tmp;
		if(!st[rt].ls)tmp=len(l,mid);
		else tmp=st[st[rt].ls].size;
		return query(st[rt].rs,mid+1,r,pos-tmp);
	}
}

void modify(int &rt,int l,int r,int pos,ll num){
	if(!rt){
		rt=++cnt;
		st[rt].size=len(l,r);
		if(l==r){
			st[rt].val=num;
		}	
	}
	
	++st[rt].size;//这个区间末尾有一个人进去
	if(l==r)return;
	
	int mid=(l+r)>>1;
	if(pos<=mid)modify(st[rt].ls,l,mid,pos,num);
	else modify(st[rt].rs,mid+1,r,pos,num);
}

inline int read() {
    int x = 0, f = 1;char ch = getchar();
    while (!isdigit(ch)) {if(ch=='-')f=-1;ch=getchar();}
    while (isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
    return x * f;
}

int main() {
#ifdef LawrenceSivan
    freopen("aa.in", "r", stdin);
    freopen("aa.out", "w", stdout);
#endif
	n=read();m=read();q=read();
	Max=max(n,m)+q;//一共有q次离队，于是最多有q个人再次进队，于是最大也就是队列长度加上他们本身（因为我们取出以后在位置进行标记，相当于占上了位置
	
	while(q--){
		int x=read(),y=read();
		if(y==m){//如果是最后一列
			now=n+1;//那么一定要放到那个单独的区间里面去，也就是上面说到的蓝色区域
			ans=query(root[now],1,Max,x); 
		}
		else{
			now=x;//否则，那么一定在红色区域
			ans=query(root[now],1,Max,y);
		} 
		
		printf("%lld\n",ans);//输出答案
		
		now=n+1;//让被选出的人进入蓝色区域的最后一个位置
		modify(root[now],1,Max,n+(++ins[now]),ans);
		
		if(y!=m){
			ans=query(root[now],1,Max,x);
			now=x;
			modify(root[now],1,Max,m-1+(++ins[now]),ans);
		}
	}
	
	return 0;
}